📓10.1: Recursion
Table of Contents
📖 This page is a condensed version of CSAwesome Topic 10.1
📓DEMO PROGRAM SETUP INSTRUCTIONS
- Go to the public template repository for our class: BWL-CS Java Template
- Click the button above the list of files then select
Create a new repository - Specify the repository name:
CS2-Unit-10-Notes - Click
Now you have your own personal copy of this starter code that you can always access under the
Your repositoriessection of GitHub! - Now on your repository, click and select the
Codespacestab - Click
Create Codespace on mainand wait for the environment to load, then you’re ready to code! - 📝 Take notes in this Codespace during class, coding along with the instructor.
What is Recursion?
Recursion in Java is when a method calls itself. Recursion is another strategy for repeating code - an alternative to loops.
- Recursive Method
- A method that contains at least one call to itself inside the method body, thereby repeating its own process recursively.
Check out more recursion visualizations!
The method below will print out “This is the method that never ends!” and then call itself, which will print out the message again, and then call itself, and so on.
public static void neverEnd() {
System.out.println("This is the method that never ends!");
neverEnd();
}
♾️ This is called infinite recursion, which is a recursion that never ends. Of course, this particular method is not very useful. (Actually, in practice it will end, crashing with a
StackOverFlowErrorbecause there is a limit on how many times you can recurse.)
The AP CSA exam usually has about 4-6 recursion problems in the MCQ section. You only need to know how to trace recursive methods, as in, figure out what they return or print. ✍️
Why Use Recursion?
Recursion is most useful for solving problems where the structure of the problem allows it to be broken into smaller but similar problems, whose solutions can be combined into the solution to the original problem.
EXAMPLES:
- 🗂️ Suppose you wanted to find out how much space a folder on your computer uses? Well, if you knew how much space each of the files and sub-folders in that folder used, you could add them up and get the answer.
- Getting the size of a regular file is usually easy, but figuring out how much space each sub-folder takes up is the same problem we stared with, just with a different folder…
- But that’s actually great news because we can use the same procedure to solve this smaller problem: find the size of all the files and sub-folders in it and add them up.
- Eventually, as we try to get the size more deeply nested folders, eventually we’ll get to folders that only contain plain files whose sizes we can add up and
return, and eventually we work our way back up to give the answer to our question about the original top-most folder.
- Recursion can also be used to create fractals.
- A simple fractal example is Sierpinski’s Triangle in which you subdivide a triangle into 4 new triangles as shown below. You can then do the same procedure with each new triangle except the center one.
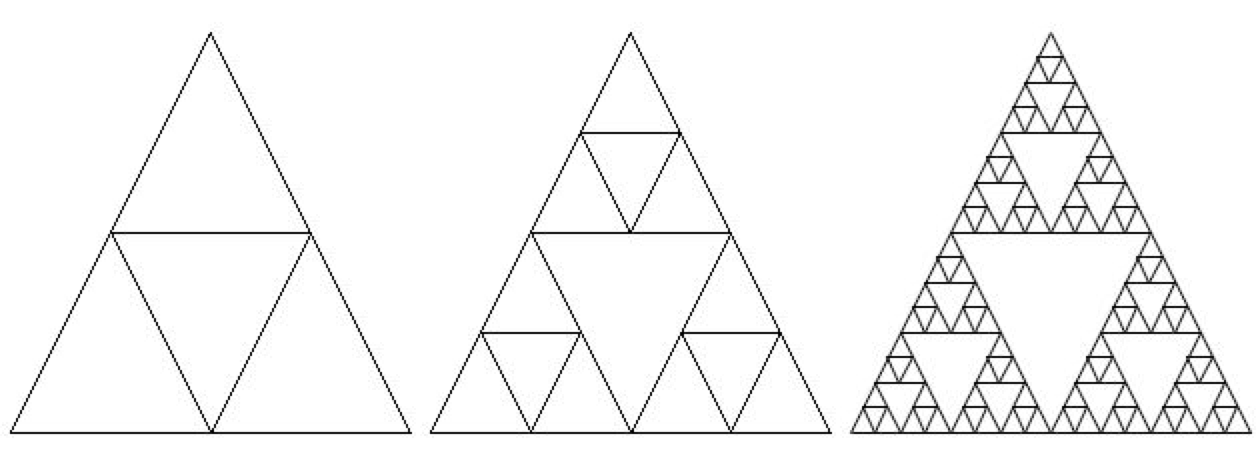
- Recursion can also be used to traverse
Strings, arrays, andArrayLists just like a loop. In fact, any loop—also known as iterative code—can be re-written using recursion!However in most languages, including Java, there are limitations on how deeply code can recurse, which rules out using recursion for infinite or even very long loops.
🌳 Recursion is more powerful than simple loops, especially when dealing with branching structures like the file folder example. Computer scientists call such data structures trees and they are incredibly common in computer programs. Thus one way to think about recursion is as “loops for trees”.
🔁 If you need to loop over a simple linear data structure like a
String, array, orArrayList, by all mean use aforloop instead of recursion. And if you want to navigate a 2D array, a pair of nestedforloops is the way to go.
Factorial Method
The following video introduces the concept of recursion and tracing recursion with the factorial method.
See the method factorial below that calculates the factorial of a number. The factorial of a number is defined as 1 for 0, and n * factorial (n-1) for any other number.
public static int factorial(int n) {
if (n == 0)
return 1;
else
return n * factorial(n-1);
}
You can also play with an interactive demonstration of the recursive factorial computation at https://gigamonkeys.com/misc/factorial/#java.
Base Case
Every non-infinite recursive method must have at least one base case as a way to stop recursion. 🛑
- Base Case
- A condition where a recursive method can
returnan answer without another recursive call. In other words, the smallest possible problem (or problems) that the method knows how to solve, the ones it can answer directly without any more recursion.
The base case is often handled by an if statement that checks for the base case condition, and returns directly when the condition for the base case is met.
-
In the factorial method: the base case is when the argument is 0 as that is the smallest number that the factorial method can handle.
-
When we recurse through folders on our computer there are TWO base cases: a simple file, whose size we can find out directly, and an empty folder whose size is 0.
The goal of every recursive call in a recursive method is to shrink the problem in some way that gets closer to the base case.
You can see that in
factorialwhere the recursive call is passingn - 1, one closer to0. This is the equivalent in recursion to incrementing your loop variable in aforloop.
The Call Stack
In Java, the call stack keeps track of the methods that you have called since the main method executes. A stack is a way of organizing data that adds and removes items only from the top of the stack.

An example is a stack of cups. You can grap a cup from the top of the stack, or add more cups at the top of the stack.
When you are executing one method (method a) and it calls another method (method b), that method call is placed on the call stack along with information about where it was called from, which tells the run-time where to return to when the current method finishes executing. When method b finishes executing, the run-time pops the method b off of the call stack and returns execution to the next line to be executed in method a.
Consider the following class definition:
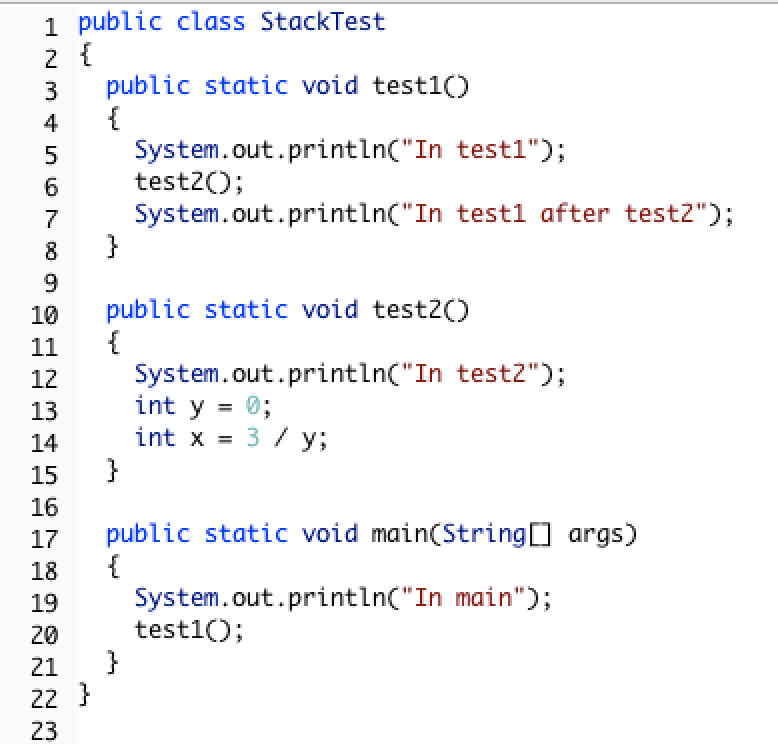
The code above will cause a run-time error of division by zero when it runs. The main method calls the method test1 (at line 20) which calls the method test2 (at line 6) which has the divide by zero error (line 14).
This error can be seen in the call stack below, which shows the call stack from the top (most recent method) to the bottom (original method call).
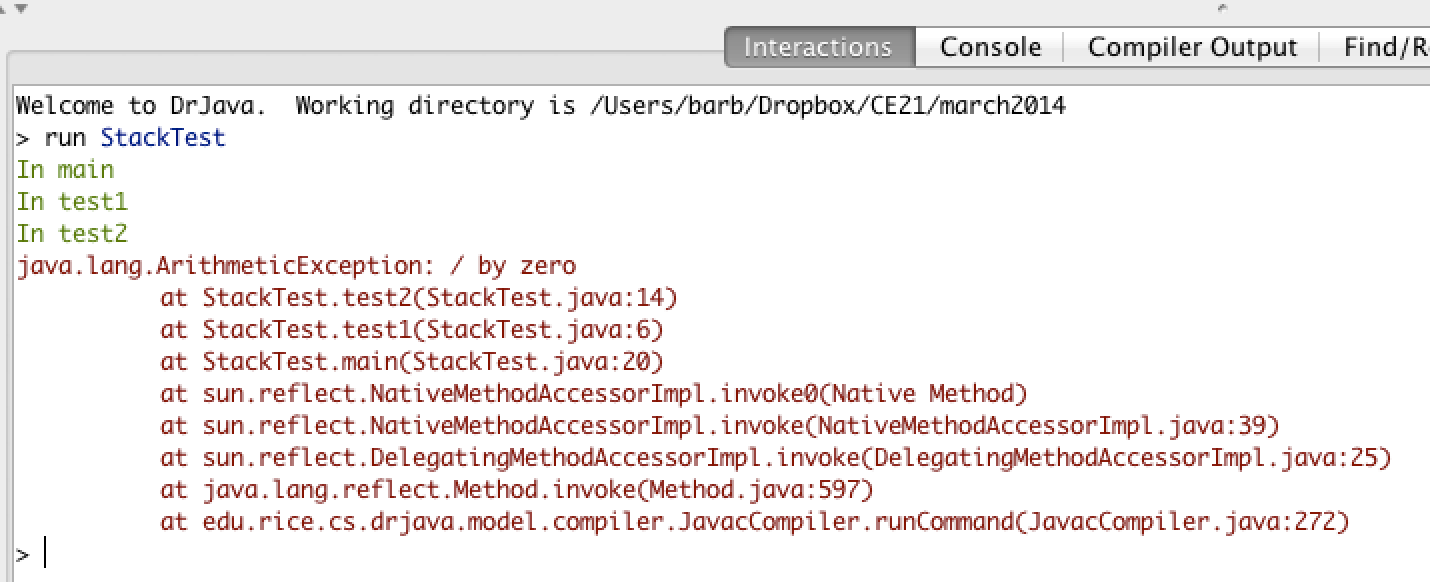
➕ When a method calls itself, the new method call gets added to the top of the call stack, taking first priority as the most recent method called. Execution of the current method pauses while the recursive call is being processed. Each recursive call on the stack has its own set of local variables, including the parameter variables. The parameter values progressively change in each recursive call until we reach the base case which stops the recursion.
Tracing Recursive Methods
Let’s trace the execution of the factorial method defined below.
public static int factorial(int n) {
if (n == 0) {
return 1;
}
else {
return n * factorial(n-1);
}
}
- What happens when we call
factorial(0)?It will return 1 (line 5) since
nis equal to 0. - How about
factorial(1)?It will return
1 * factorial(0). We already know thatfactorial(0)returns 1, but the computer won’t remember that. It will executefactorial(0)and return the result (1). Sofactorial(1)returns1 * 1, which is1.
How can you show what is happening in a recursive call? The lines below show the call stack upside down (with the bottom of the stack, or the original call at the top and the most recent call at the bottom) for a call to factorial(5).
✍️ This is a handy way to trace a recursive method on the exam!!!
factorial(5) returns 5 * factorial(4)
factorial(4) returns 4 * factorial(3)
factorial(3) returns 3 * factorial(2)
factorial(2) returns 2 * factorial(1)
factorial(1) returns 1 * factorial(0)
factorial(0) returns 1
Once factorial(0) executes and returns 1, that value can be substituted back into the previous method call, starting at the top of the stack (shown at the bottom here) and working our way back to the bottom of the stack (shown at the top here).
factorial(5) returns 5 * factorial(4) = 5 * 24 = 120
factorial(4) returns 4 * factorial(3) = 4 * 6 = 24
factorial(3) returns 3 * factorial(2) = 3 * 2 = 6
factorial(2) returns 2 * factorial(1) = 2 * 1 = 2
factorial(1) returns 1 * factorial(0) = 1 * 1 = 1
factorial(0) returns 1
So factorial(5) returns 120, as the final solution to the original question.
✍️ Trace the execution of the bunny ears method defined below:
public static int bunnyEars(int bunnies) {
if (bunnies == 0) {
return 0;
}
else if (bunnies == 1) {
return 2;
}
else {
return 2 + bunnyEars(bunnies - 1);
}
}
- What happens when we call
bunnyEars(0)?It will return 0 since
nis equal to 0. - How about
bunnyEars(1)?It will return 2 since
nis equal to 1. - What about
bunnyEars(5)?
✅ CHECK YOUR SOLUTION:
bunnyEars(5) returns 2 + bunnyEars(4)
bunnyEars(4) returns 2 + bunnyEars(3)
bunnyEars(3) returns 2 + bunnyEars(2)
bunnyEars(2) returns 2 + bunnyEars(1)
bunnyEars(1) returns 2
This approach shows the call stack from bottom to top. Once bunnyEars(1) executes and returns 2 that value can be substituted back into the previous method call, starting at the top and working our way back toward the bottom (or beginning) of the call stack.
bunnyEars(5) returns 2 + bunnyEars(4) = 2 + 8 = 10
bunnyEars(4) returns 2 + bunnyEars(3) = 2 + 6 = 8
bunnyEars(3) returns 2 + bunnyEars(2) = 2 + 4 = 6
bunnyEars(2) returns 2 + bunnyEars(1) = 2 + 2 = 4
bunnyEars(1) returns 2
So bunnyEars(5) returns 10.
⭐️ Summary
-
Recursive Method - A method that contains at least one call to itself inside the method.
-
Base Case - A way to stop the recursive calls. This is a return statement without a recursive call.
-
Call Stack - The call stack keeps track of the methods that are called while the code executes. It keeps track of the local variables and where the call will return to.
🛑 When class ends, don’t forget to SAVE YOUR WORK!
- Navigate to the
Source Controlmenu on the LEFT sidebar - Type a brief commit message in the box, for example:
updated Main.java - Click the button on the LEFT menu
- Click the button on the LEFT menu
- Finally you can close your Codespace!
Acknowledgement
Content on this page is adapted from Runestone Academy - Barb Ericson, Beryl Hoffman, Peter Seibel.